前言：算法其实是人类逻辑的“镜像”#

很多人觉得算法高不可攀，但翻开西瓜书第四章，你会发现 决策树（Decision Tree） 其实就是我们脑海里那个“if-else”的自动化版本。它没有复杂的梯度、没有难懂的核函数，它只有一种“打破砂锅问到底”的执着。

决策树的基本流程#

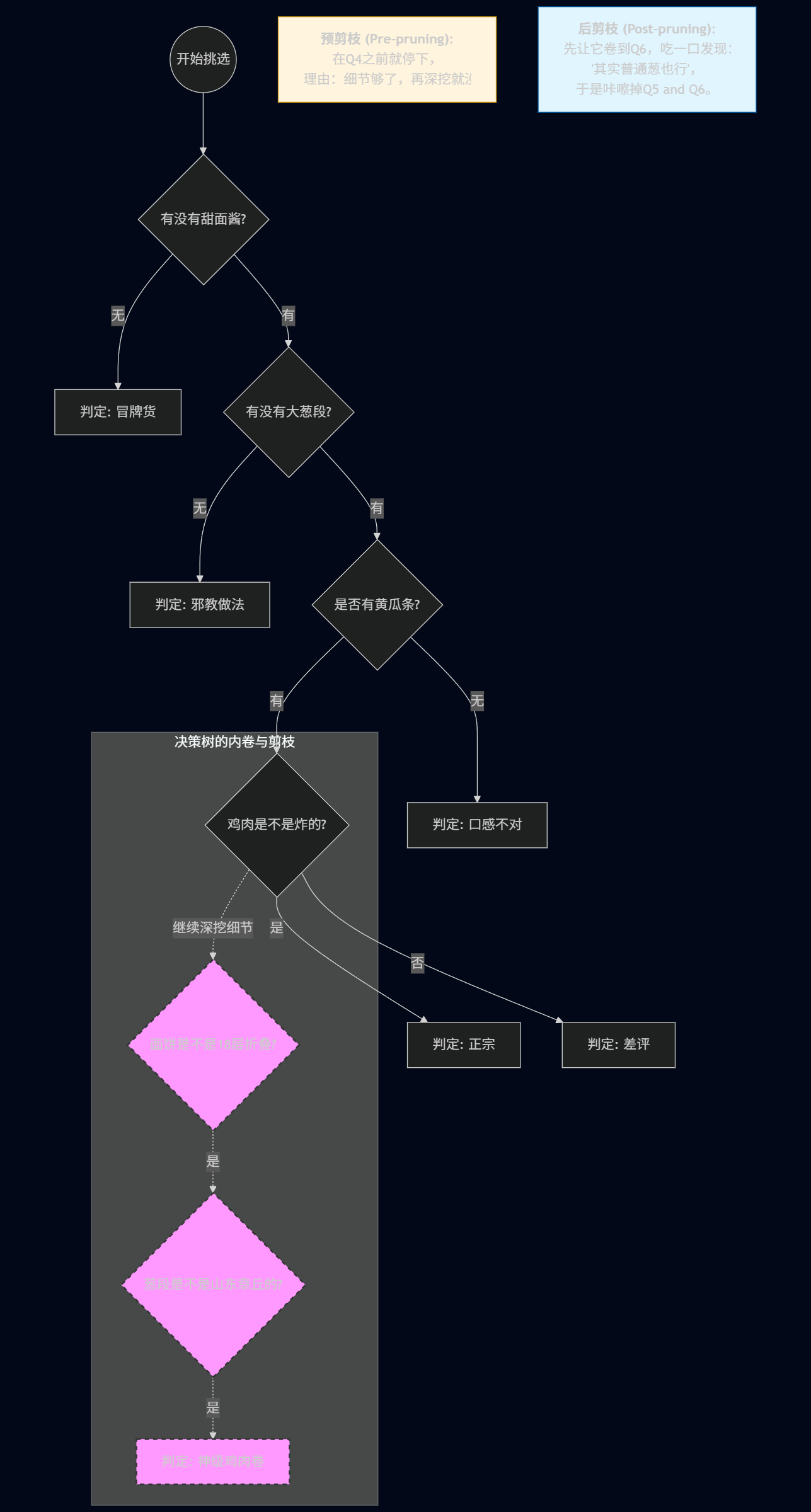
想象你在广州的城中村找一家好吃的炸鸡店。你脑子里其实有一张树状图：

但在算法的世界里，这场“问答游戏”不能无休止玩下去，有三种情况得提前“收工”（递归返回）：

Decision tree algorithm flowchart

决策树每一步都在选那个 “最有含金量” 的问题。为了量化这个“含金量”，数学家们搬出了几个工具：

如果你的炸鸡桶里一半是极品，一半是过期货，那这个桶的信息熵最高（最混乱）。

Ent(D) = -\sum_{k=1}^{|Y|} p_k \log_2 p_k

当所有类别概率相等时，熵最大；当全桶只有一种货色时，熵为 0。

信息增益：问了这个问题后，比起没问之前，你的“混乱度”减少了多少。
增益率：为了防止模型变成“势利眼”。比如有个属性叫“订单号”，它能把每个样本分得极纯，但这没意义。增益率通过 “固有值” 给了这种分支过多的属性一个“惩罚”。

就像在舞池里随机抓两个人，如果他们“种类不一样”的概率越低，说明纯度越高。CART 树就是靠这个基尼指数来找最优划分点的。

算法流派	核心武器 (指标)	擅长领域/气质	避坑指南 (缺点)
ID3	信息增益 (Gain)	纯粹的分类，适合逻辑简单的“老字号”	容易被“订单号”这种分得很细、但没意义的属性带节奏。
C4.5	增益率 (Gain Ratio)	追求公平的“平衡大师”，能处理连续值	虽然更全面，但计算熵时涉及对数运算，比别的算法累一点。
CART	基尼指数 (Gini)	极简主义，只搞二叉树，分类/回归都能打	最爱“扎堆”，效率极高，是现在很多主流框架的“默认配置”。

这就是我们之前提到的“老王手抖”问题（过拟合）。如果决策树学得太细，把炸鸡粉里的一个气泡都当成判断标准，那这模型就废了。

如果老王在复刻“老北京鸡肉卷”时，不仅学到了甜面酱和大葱的比例，还非要学着总部大厨放葱时的手势角度、甚至当天的空气湿度。这棵决策树就“卷”过头了。它在总部后厨表现完美，但换到你自己店里，可能就因为你没法复现那些无意义的细节而彻底翻车。

在孩子钻牛角尖之前，提前喊停。

让模型先疯长，然后家长拿把剪刀，把那些“没用且费劲”的分支喀嚓掉。

逻辑：先让这棵树卷到极致，卷到连“葱段是不是章丘产的”都要判断。然后根据验证集的数据，从下往上回溯：如果把这个细枝末节剪掉，效果反而更好或没差，那就果断“咔嚓”。
效果：虽然累点，但它保留了经过实战检验的最稳逻辑。
代价：时间成本高，就像先让孩子把所有弯路走一遍，再来总结人生经验。

现实世界不是 0 和 1 那么简单，总有数据在“掉链子”：

连续值（如炸鸡重量）：不能每个重量都分一类，我们会找一个黄金分割点（二分法）。比如 200g 是个坎，过了这个坎就是“大份”，没过就是“小份”。
缺失值（如老板记性不好）：
- 谁也没法学：属性缺失了，那我们在计算“含金量”时，就只看那些有数据的样本，并给它们一个权重 $\rho$ 。
- 雨露均沾：如果一个样本缺失了某个属性，我们就按比例把它分发到所有分支里，只是它的“话语权”（权重）变轻了。