前言
如果说神经网络是复杂的后厨绩效系统,那么支持向量机(SVM)就是一位极简主义的“金牌质检员”。
在第五章中我们聊过,感知机(Perceptron)只要能把“好鸡肉卷”和“坏鸡肉卷”分开放就行,所以它的解有无数个。但 SVM 不同,它是个极简主义的完美主义者:它要求这条线必须位于正负样本的正中间,且间隔(Margin)最大。
间隔与支持向量:追求绝对的“稳”
1.1 超平面的几何定义
在 维空间中,划分超平面的方程为:
- 法向量 :决定了超平面的方向。
- 位移项 :决定了超平面离原点的距离。
1.2 距离的真相:为什么 越小间隔越大?
任意点 到超平面的几何距离为:
为了让解唯一,我们施加约束:令离超平面最近的样本(即支持向量)满足 。
此时,正负支持向量之间的总距离(间隔 )就是:
结论想要间隔 最大,就等价于最小化 。
对偶问题:后厨经理的“资源最优解”
直接求解最小化 很直观,但为了引入核函数并提升效率,我们需要通过 拉格朗日对偶(Lagrangian Duality) 将其转化。
碎碎念在推导对偶问题时,你会发现 。这个公式非常美——它说明最终的“正义边界”其实就是由支持向量加权组合而成的。
2.1 构造拉格朗日函数
我们将约束条件 引入目标函数:
其中 是拉格朗日乘子。
2.2 KKT 条件:最优化的“合同条款”
在最小值点,必须满足 KKT 条件。其中最浪漫的是互补松弛性(Complementary Slackness):
这意味着:
- 如果 ,那么该样本必须在边界上(即 ),它就是支持向量。
- 如果样本不在边界上,那么它的 必须为 ,对最终模型的构建毫无贡献。
换而言之SVM 告诉我们,决定大局的永远是那些处于边界、最难处理的“少数派”。
核函数:给口味升个维度(Kernel Trick)
3.1 空间映射的艺术:给口味“升个维度”
如果炸鸡的口味需求是“异或”逻辑(如:只要辣或只要蒜,但不能都要),这把叫感知机的“直刀”在二维平面上就彻底断了。这时候,SVM 展现了它最神奇的招数:空间映射。
3.1.1 什么是映射 ?
想象一下,那些纠缠在一起、无法用直线分开的红豆和绿豆。如果我们用力拍一下桌子,让豆子们弹到空中——在它们飞起来的那个瞬间,原本在桌面上重叠的豆子,在高度这个“第三维度”上就被分开了。
在数学上,我们用 将低维空间的输入 投射到高维特征空间。
碎碎念我一直觉得线性代数最浪漫的地方就在于此:有些矛盾在低维空间是死结,但只要你提升一个维度,世界就豁然开朗。这不仅是数学,也是一种解决问题的哲学。
3.2 核技巧 (Kernel Trick):计算上的“偷梁换柱”
如果我们真的去计算高维映射 ,那麻烦就大了:
- 维度灾难:如果映射到无穷维,电脑内存会直接爆炸。
- 计算量惊人:高维向量的内积运算会慢到让你怀疑人生。
核函数 的伟大之处在于:它是一条“虫洞”。它告诉我们:你不需要真的知道高维空间长什么样,你只需要知道两个点在高维空间里的“相似度”(内积)是多少。
我们直接在低维空间计算 ,其结果竟然等价于高维空间的 。这就像是你不需要真的去造一个三维模型,只需要通过一个特殊的公式,就能提前预知它们在三维空间里的距离。这就是著名的 Kernel Trick。
3.2.1 常见核函数“菜单”
| 核函数名称 | 数学表达式 | 核心参数 | 学习特征 (Learning Bias) | 适用场景 |
|---|---|---|---|---|
| 线性核 (Linear) | 无 | 假设数据线性可分,属于高偏差、低方差模型。 | 原始特征维度极高时(如文本分类、基因数据)。 | |
| 多项式核 (Poly) | (阶数), (位移) | 映射到 维空间,阶数越高,边界越复杂。 | 处理具有明显特征组合关系的低维数据。 | |
| 高斯核 / RBF | 万能逼近器。映射到无穷维空间,极易过拟合。 | 首选通用核。适用于大多数无先验知识的非线性数据。 | ||
| 拉普拉斯核 | 对 RBF 的变体,对参数变化更敏感,边界更尖锐。 | 图像处理中对边缘敏感的场景。 | ||
| Sigmoid 核 | 使得 SVM 的数学形式等价于一个单层感知机。 | 深度学习早期研究中作为网络节点的替代。 |
Mercer 定理为什么我们可以随便发明核函数?因为数学家 Mercer 证明了:只要一个对称函数对应的核矩阵是半正定的,它就能作为核函数使用。这给了我们极大的自由度去定制属于自己的“空间跳跃”规则。
软间隔与正则化:允许“偶尔烧焦”
现实中,数据总有噪声。如果硬要完全分对,模型会变得极其扭曲(过拟合)。
4.1 容忍度 :完美主义与务实主义的博弈
在现实世界里,数据往往是“脏”的。有些废品炸鸡可能长得非常像金牌炸鸡(噪声数据)。如果我们死磕硬间隔(Hard Margin),非要画出一条绝对完美的线,模型就会为了迁就那一两个“害群之马”而变得极其扭曲,这就是过拟合(Overfitting)。
为了解决这个问题,我们引入了松弛变量 ,允许部分样本稍微“越界”。此时,优化目标变成了:
这里的 就是老板的“容忍度度量衡”:
- 很大(完美主义):老板眼里容不得沙子。只要有一个学徒偷懒,哪怕模型变得九曲十八弯也要惩罚。后果是模型可能只记住了这批数据的毛病,换批炸鸡就不灵了。
- 很小(务实主义):老板很大度,觉得“偶尔烧焦一两块在所难免”。他更看重整体边界的平滑。这样画出来的线泛化性能更好,能适应未来的各种突发状况。
4.2 殊途同归:SVM 与对数几率回归的“秘密条约”
很多初学者觉得 SVM 和我们在第三章聊过的 对数几率回归(Logistic Regression) 是两家店,但如果你扒开它们的数学底裤,你会发现它们其实是“异父异母的亲兄弟”。
4.2.1 损失函数的博弈
SVM 的核心是 Hinge Loss(折页损失),而对数几率回归用的是 对率损失(Logistic Loss)。
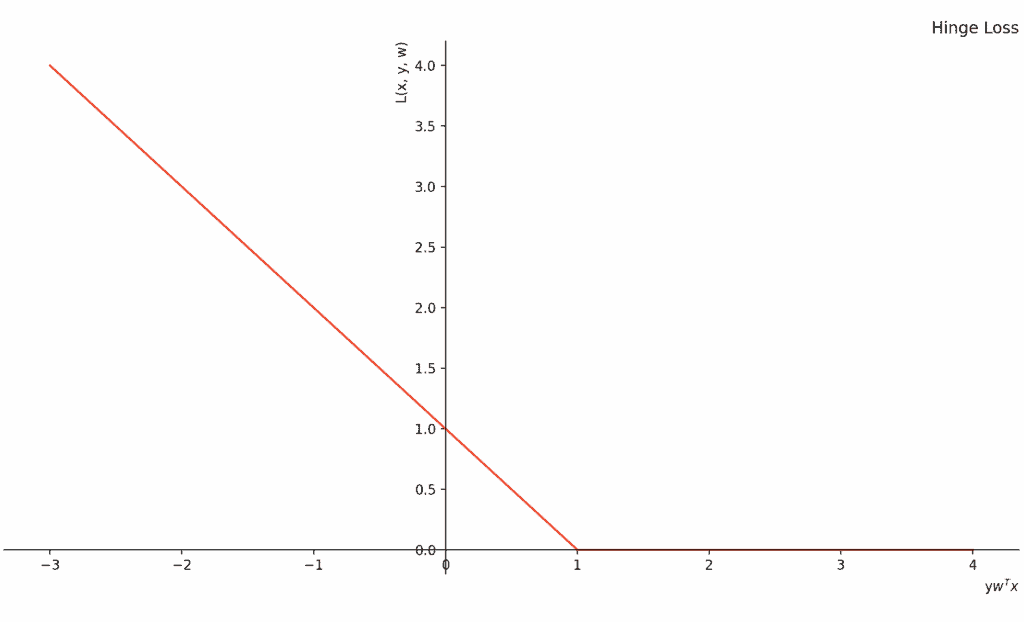
Hinge Loss折页损失

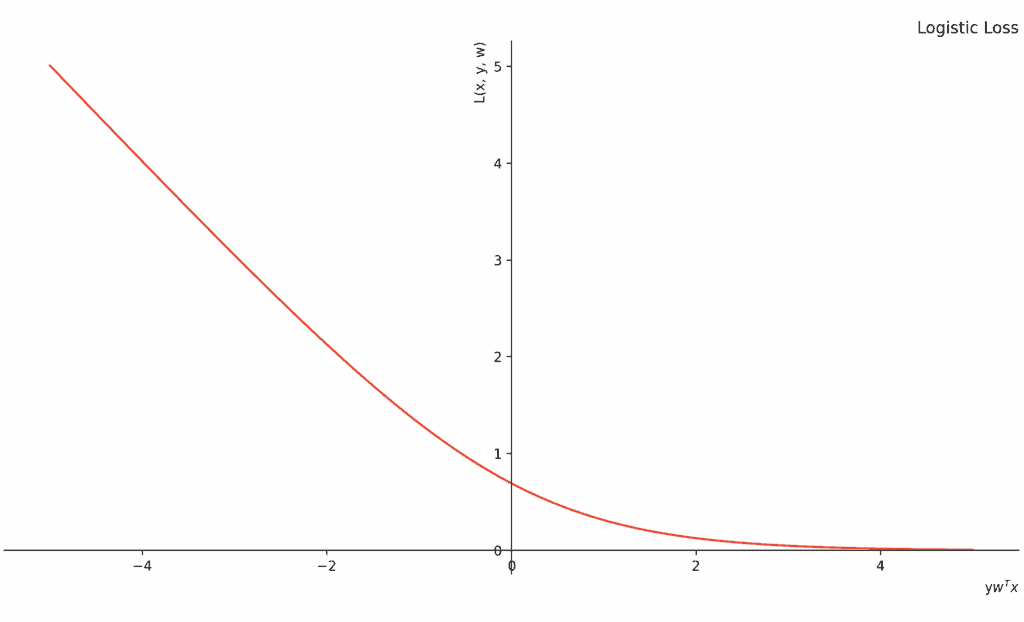
Logistic Loss对数损失
我们可以通过下表更清晰地看到这两位“质检员”的性格差异(参见Differences Between Hinge Loss and Logistic Loss | Baeldung on Computer Science)
我们有以下表格:
| 特性 | Hinge Loss (SVM) | Logistic Loss (LR) |
|---|---|---|
| 凸性 (Convexity) | ✓ (都是好优化的“碗状”) | ✓ (都是好优化的“碗状”) |
| 可微性与平滑度 | ✗ (在 处有“硬转折”) | ✓ (处处平滑可导) |
| 稀疏性 (Sparsity) | ✓ (核心优势,只看支持向量) | ✗ (所有样本都会参与运算) |
| 计算开销 | ✓ (更便宜,计算量小) | ✗ (相对略高) |
| 潜在精度 | ✓ (通常表现更稳健) | ✗ (容易受噪声干扰) |
| 概率校准 (Calibration) | ✗ (输出是分数,不是概率) | ✓ (天然输出置信概率) |
如果我们把对数几率回归的标签从 换成 SVM 习惯的 ,它的损失函数公式可以改写为:
这跟软间隔 SVM 的优化目标在形式上极其神似。两者的区别在于:
-
Hinge Loss 的冷酷(✓ Sparsity):
注意到 Hinge Loss 的图像在 之后就变成了一条水平的直线(值为 0)。这意味着,只要炸鸡已经足够优秀(完全达标),它对梯度的贡献就是 0。这使得我们的模型最终只需要存储极少数的支持向量。这对于大规模数据来说,不仅节省了内存,还极大提升了预测速度。
-
Logistic Loss 的纠缠(✗ Sparsity):
对数几率回归的损失函数是一个永远不会真正到达 0 的长尾巴。哪怕一块鸡已经完美得无可挑剔,它依然会产生一点点微小的损失,强迫模型去关注它。这种“雨露均沾”的策略虽然让概率预测更准,但在处理海量数据时,会显得非常臃肿。
4.3 为什么 SVM 往往表现更好?
这就涉及到了结构风险最小化。
SVM 的优化目标里自带了 。在数学上,这不仅是为了算间隔,更是一种 L2 正则化。它天然地在寻找那个最简单的模型(法向量模长最小),从而有效压制了过拟合。
小心得对数几率回归像是要讨好所有顾客,给出一个全场平均分;而 SVM 则像是一个只盯着“差生”和“边缘生”的班主任。只要把最难搞的那些“支持向量”搞定了,整个炸鸡店的质量标准就稳了。
支持向量回归 (SVR):带“护城河”的回归
SVM 不仅能分类,还能预测价格(回归)。
不同于普通回归要求线必须穿过点,SVR 构建了一个宽度为 的间隔带。
只要样本落在带子内,我们就认为预测准确,不计损失。只有跑出带子的“离群炸鸡”,才会产生损失。这种 -不敏感损失函数让 SVR 面对异常数据时稳如老狗。
结语:寻找全局最小的“黄金分割”
SVM 的美感在于它的确定性。在复杂的决策中,不要试图讨好每一个数据点,守住最核心的“支持向量”,你就能画出那条通往全局最优的黄金分割线。
该专题下还有 4 篇相关笔记,点击继续探索:
